20. 某人在双休日骑电动自行车到海滨、连岛观光,途经全长 6 700 m、被人们称为“神州第一堤”的连云港拦海大堤。设电动自行车以 18 km/h 的速度匀速行驶,其电动机的功率为 150 W。求:
(1)该人通过大堤全程所需的时间;
(2)电动自行车通过大堤全程牵引力所做的功;
(3)电动自行车的牵引力。
答案:$(1)$ 计算通过大堤全程所需的时间
解:已知电动自行车速度$v = 18km/h = 18×\frac{1000m}{3600s}= 5m/s$,路程$s = 6700m$。
根据公式$t=\frac{s}{v}$(速度公式变形),可得通过大堤全程所需时间$t=\frac{6700m}{5m/s}=1340s$。
$(2)$ 计算电动自行车通过大堤全程牵引力所做的功
解:已知电动机功率$P = 150W$,时间$t = 1340s$。
根据公式$W = Pt$(功率公式变形$P=\frac{W}{t}$),可得牵引力所做的功$W=150W×1340s = 2.01×10^{5}J$。
$(3)$ 计算电动自行车的牵引力
解:已知$W = 2.01×10^{5}J$,$s = 6700m$。
根据公式$F=\frac{W}{s}$(功的公式$W = Fs$变形),可得牵引力$F=\frac{2.01×10^{5}J}{6700m}=30N$。
综上,答案依次为:$(1)$$\boldsymbol{1340s}$;$(2)$$\boldsymbol{2.01×10^{5}J}$;$(3)$$\boldsymbol{30N}$ 。
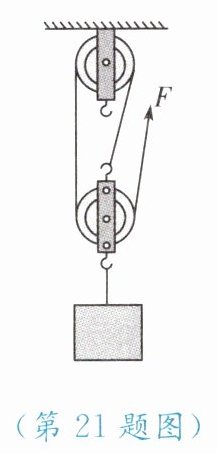
21. 工人用如图所示的滑轮组在 10 s 内将 240 N 的物体匀速提升了 2 m,已知工人的拉力 F=100 N,不计绳重与摩擦阻力,问:
(1)工人做功的功率是多少?
(2)滑轮组的机械效率是多少?
(3)如果用此滑轮组匀速提升 300 N 的重物,那么机械效率变为多大?
答案:解:$(1)s=3h=3×2\ \text {m}=6\ \text {m}$
$ W=Fs={ 100 }\ \text{N}×{ 6 }\ \text{m}={ 600 }\ \text{J}$
$ P=\frac {W}{t}=\frac {{ 600 }\ \text{J}}{{ 10 }\ \text{s}}={ 60 }\ \text{W}$
$ (2)W_{有}=Gh={ 240 }\ \text {N}×{ 2 }\ \text {m}={ 480 }\ \text {J}$
$ η=\frac {W_{有}}{W}×100\%=\frac {{ 480 }\ \text{J}}{{ 600 }\ \text{J}}×100\%={ 80 }\%$
$ (3)G_{动}=3F-G=3×100\ \text {N}-240\ \text {N}=60\ \text {N}$
$ η'=\frac {G'}{G'+G_{动}}=\frac {300\ \text {N}}{300\ \text {N}+60\ \text {N}}×100\%≈83.3\%$