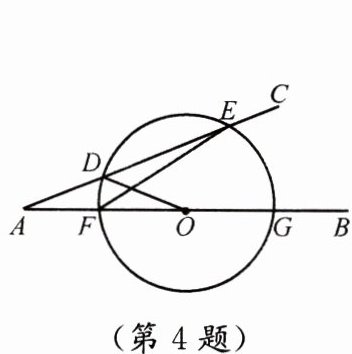
4. 如图,$D为AC$上的一点,$O为AB$上的一点,$AD = DO$.以点$O$为圆心,$OD$的长为半径画圆,交$AC于点E$,交$AB于点F$、$G$,连接$EF$.若$\angle BAC = 22^{\circ}$,则$\angle EFG = $
33°
.
答案:33°
解析:
在△ADO中,AD=DO,∠DAO=∠BAC=22°,故∠AOD=∠DAO=22°,∠ADO=180°-22°-22°=136°。
∵∠ADO+∠ODE=180°(平角定义),∴∠ODE=180°-136°=44°。
∵OD=OE(半径相等),∴∠OED=∠ODE=44°,∠DOE=180°-44°-44°=92°。
∠AOE=∠AOD+∠DOE=22°+92°=114°。
∵A、O、G共线,∴∠EOG=180°-∠AOE=180°-114°=66°。
∠EFG为圆周角,所对弧为EG,故∠EFG=1/2∠EOG=1/2×66°=33°。
5. 如图,$\odot B的圆心在y$轴的负半轴上,半径为$5$.$\odot B与y轴的正半轴交于点A(0,1)$,过点$P(0, - 7)的直线l与\odot B相交于C$、$D$两点,则弦$CD$长的所有可能的整数值有______
3
个.

答案:3
解析:
1. 确定圆心B坐标:圆心在y轴负半轴,设B(0,b)。A(0,1)在圆上,半径5,故|1 - b| = 5,解得b = -4,即B(0,-4)。
2. 计算BP距离:P(0,-7),B(0,-4),BP = |-4 - (-7)| = 3。
3. 弦长范围:过P的弦中,最长为直径10;最短弦垂直于BP,此时弦心距d = BP = 3,最短弦长=2√(5² - 3²)=8。
4. 整数值:弦长CD取值范围[8,10],整数值为8,9,10,共3个。
6. 已知:如图,$AB为\odot O$的直径,$AB = AC$,$BC交\odot O于点D$,$AC交\odot O于点E$,$\angle BAC = 45^{\circ}$.
(1) 求$\angle EBC$的度数;
(2) 求证:$BD = CD$.

答案:(1) ∵AB是⊙O直径,∴∠AEB=90°(直径所对圆周角是直角)。
在Rt△ABE中,∠BAC=45°,∴∠ABE=90°-∠BAC=45°。
∵AB=AC,∴∠ABC=∠ACB。
∵∠BAC=45°,∴∠ABC=(180°-45°)/2=67.5°。
∴∠EBC=∠ABC-∠ABE=67.5°-45°=22.5°。
(2) 连接AD。
∵AB是⊙O直径,D在⊙O上,∴∠ADB=90°(直径所对圆周角是直角),即AD⊥BC。
∵AB=AC,AD⊥BC,∴BD=CD(等腰三角形三线合一)。
1. 如图,某公路的转弯处可以看作一段圆弧(即$\overset{\LARGE{\frown}}{CD}$,$O是\overset{\LARGE{\frown}}{CD}$所在圆的圆心),$CD = 600m$,$E为\overset{\LARGE{\frown}}{CD}$上一点,且$OE\perp CD$,垂足为$F$,$OF = 300\sqrt{3}m$,则这段弯路的长度为(
A
)

A.$200\pi m$
B.$100\pi m$
C.$400\pi m$
D.$300\pi m$
答案:A
解析:
由于$OE \perp CD$,根据垂径定理,$F$为$CD$中点,所以$CF=\frac{1}{2}CD = 300m$。
在$Rt\triangle COF$中,$OC$为半径$R$,$OF = 300\sqrt{3}m$,由勾股定理$R^{2}=CF^{2}+OF^{2}$,即$R^{2}=300^{2}+(300\sqrt{3})^{2}=300^{2}(1 + 3)=300^{2}×4$,所以$R = 600m$。
设$\angle COF=\alpha$,$\tan\alpha=\frac{CF}{OF}=\frac{300}{300\sqrt{3}}=\frac{\sqrt{3}}{3}$,则$\alpha = 30^{\circ}$,那么$\angle COD = 60^{\circ}$,$\angle COD$对应的圆心角$\theta=60×\frac{\pi}{180}=\frac{\pi}{3}$(弧度)。
根据弧长公式$l = R\theta$,可得弧长$l=600×\frac{\pi}{3}=200\pi m$。
2. 如图是由$7$个形状、大小完全相同的正六边形组成的网格,正六边形的顶点称为格点.已知$\triangle ABC$的顶点都在格点上,且边$AB$如图所示,则是直角三角形的$\triangle ABC$有(
C
)

A.$4$个
B.$6$个
C.$8$个
D.$10$个
答案:C
解析:
以AB为边,分三种情况讨论直角三角形:
1. 直角顶点为A:AC⊥AB,根据正六边形网格向量垂直条件,得C点坐标满足$y=-2x$,网格内有$(-1,2)$、$(1,-2)$,共2个。
2. 直角顶点为B:BC⊥BA,同理得C点坐标满足$y=-2x+4$,网格内有$(1,2)$、$(3,-2)$,共2个。
3. 直角顶点为C:AC⊥BC,由勾股定理逆定理$AC²+BC²=AB²$($AB²=4$),解得$AC²=1,BC²=3$或$AC²=3,BC²=1$,网格内有$(0,1)$、$(1,-1)$、$(1,1)$、$(2,-1)$,共4个。
综上,共有$2+2+4=8$个直角三角形。