1. 若点 $ A $ 在 $ \odot O $ 上,过点 $ A $ 画 $ \odot O $ 的切线,能画几条?
答案:1. 因为点A在⊙O上,根据切线的性质定理:经过半径的外端并且垂直于这条半径的直线是圆的切线。
2. 过点A只能作一条直线垂直于OA(OA为半径)。
3. 所以过点A能画1条⊙O的切线。
结论:1条
2. 如图 $ 2 - 19 $,三角尺的直角顶点 $ A $ 在 $ \odot O $ 上,一条直角边经过圆心 $ O $,另一条直角边经过 $ \odot O $ 外一点 $ P $,$ PA $ 是 $ \odot O $ 的切线吗?为什么?
答案:PA是⊙O的切线。
理由:连接OA。
∵点A在⊙O上,
∴OA是⊙O的半径。
∵∠PAO=90°(三角尺的直角顶点为A),
∴OA⊥PA。
∵OA是⊙O的半径,且OA⊥PA,
∴PA是⊙O的切线(切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线)。
答案:能画2条。
画法:
1. 连接OP;
2. 以OP为直径作圆,与已知圆交于A、B两点;
3. 连接PA、PB。
则PA、PB即为所求切线。
1. 如图 $ 2 - 21 $,$ PA $ 为 $ \odot O $ 的一条切线,切点为 $ A $. 沿直线 $ PO $ 将 $ \odot O $ 对折,由于 $ PO $ 经过圆心 $ O $,所以 $ PO $ 是圆的一条对称轴. 设点 $ B $ 落在点 $ A $ 上,$ OB $ 是 $ \odot O $ 的一条
半径
,$ PB $ 是 $ \odot O $ 的一条
切线
.
答案:半径,切线
解析:
根据题意,$PA$ 是 $\odot O$ 的切线,切点为 $A$,根据切线的性质可知 $OA \perp PA$。
沿直线 $PO$ 对折 $\odot O$,$PO$ 是圆的对称轴,点$B$落在点$A$上,则$OB$为半径;
由于对称性质,$PB$与$PA$重合(在对折意义下),即$PB$也与$OA$垂直,且$PB$与圆相交于一点(即$B$点,也是$A$点的对称点),所以$PB$是圆的切线。
2. 在上述操作中,若 $ PO $ 交 $ \odot O $ 于点 $ C $、$ D $,图中有哪些相等关系?怎样证明这些相等关系?
答案:1. 首先分析相等关系:
相等关系有:$PA = PB$,$\angle APO=\angle BPO$,$\overset{\frown}{AC}=\overset{\frown}{BC}$,$\overset{\frown}{AD}=\overset{\frown}{BD}$。
2. 然后证明$PA = PB$,$\angle APO=\angle BPO$:
连接$OA$,$OB$。
因为$PA$,$PB$是$\odot O$的切线,所以$OA\perp PA$,$OB\perp PB$(切线的性质:圆的切线垂直于经过切点的半径),即$\angle OAP = \angle OBP=90^{\circ}$。
又因为$OA = OB$(同圆的半径相等),$OP = OP$(公共边)。
在$Rt\triangle OAP$和$Rt\triangle OBP$中,根据$HL$(斜边 - 直角边)定理:
$Rt\triangle OAP\cong Rt\triangle OBP$($\left\{\begin{array}{l}OA = OB\\OP = OP\end{array}\right.$)。
所以$PA = PB$,$\angle APO=\angle BPO$(全等三角形的对应边相等,对应角相等)。
3. 接着证明$\overset{\frown}{AC}=\overset{\frown}{BC}$,$\overset{\frown}{AD}=\overset{\frown}{BD}$:
因为$\angle APO=\angle BPO$,$OA = OB$,$OC = OA$,$OD = OB$(同圆半径相等)。
根据圆心角、弧、弦之间的关系:在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等。
连接$OC$,$OD$,$\angle AOC = 2\angle APO$,$\angle BOC = 2\angle BPO$(圆心角与圆周角的关系:同弧所对的圆心角是圆周角的$2$倍,这里$PA$,$PB$是切线,$\angle OAP=\angle OBP = 90^{\circ}$,$\angle AOC$与$\angle APO$,$\angle BOC$与$\angle BPO$存在这样的关系)。
由于$\angle APO=\angle BPO$,所以$\angle AOC=\angle BOC$,则$\overset{\frown}{AC}=\overset{\frown}{BC}$(在同圆中,相等的圆心角所对的弧相等)。
又因为$\angle AOD = 180^{\circ}-\angle AOC$,$\angle BOD = 180^{\circ}-\angle BOC$,所以$\angle AOD=\angle BOD$,则$\overset{\frown}{AD}=\overset{\frown}{BD}$(在同圆中,相等的圆心角所对的弧相等)。
综上,相等关系为$PA = PB$,$\angle APO=\angle BPO$,$\overset{\frown}{AC}=\overset{\frown}{BC}$,$\overset{\frown}{AD}=\overset{\frown}{BD}$;证明过程如上述。
解析:
由于题目中未给出“上述操作”的具体内容及图形,无法确定图中相等关系及证明过程,故无法作答。1
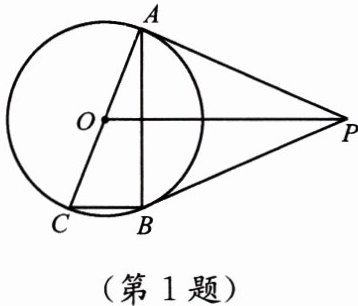
1. 如图,$ PA $、$ PB $ 是 $ \odot O $ 的两条切线,切点分别为 $ A $、$ B $,$ AC $ 是 $ \odot O $ 的直径,连接 $ AB $、$ BC $、$ OP $,图中与 $ \angle AOP $ 相等的角有(
D
)
A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 5 $ 个
答案:D
解析:
∵PA、PB是⊙O切线,∴OA⊥PA,OB⊥PB,PA=PB,OP平分∠APB且OP垂直平分AB(切线长定理).
∵OA=OB,∴OP平分∠AOB,即∠AOP=∠BOP(1个).
∵AC是直径,∴∠ABC=90°(直径所对圆周角).
∵OP⊥AB,设垂足为D,则∠OAD+∠AOP=90°,又∠OAD+∠PAB=90°(∠OAP=90°),∴∠AOP=∠PAB(2个).
∵PA=PB,∴∠PAB=∠PBA,故∠AOP=∠PBA(3个).
∵∠ABC=90°,∠OBA=∠OAB=90°-∠AOP,∴∠OBC=90°-∠OBA=∠AOP(4个).
∵OB=OC,∴∠OBC=∠ACB,故∠AOP=∠ACB(5个).
综上,与∠AOP相等的角有∠BOP、∠PAB、∠PBA、∠OBC、∠ACB,共5个.
2. 从圆外一点 $ P $ 向半径为 $ 9 \, cm $ 的圆画切线,所得切线长为 $ 18 \, cm $,则点 $ P $ 与圆上各点所连线段中最短的一条长为
9√5 - 9
$ cm $.
答案:9√5 - 9
解析:
设圆心为O,切点为A,连接OA、OP。
∵PA是切线,∴OA⊥PA,OA=9cm,PA=18cm。
在Rt△POA中,OP²=OA²+PA²=9²+18²=81+324=405,∴OP=√405=9√5 cm。
点P与圆上各点所连线段中最短的长为OP - OA = 9√5 - 9 cm。