1. 由勾股定理可得问题中数量之间的相等关系是
$a^{2} + b^{2} = c^{2}$
。
答案:$a^{2} + b^{2} = c^{2}$
解析:
勾股定理主要用于直角三角形中,描述三边之间的数量关系,即直角三角形中两条直角边(直角对应的两条边)的平方和等于斜边(直角三角形中最长的边,即斜对直角角的边)的平方。
根据勾股定理,设直角三角形的两条直角边分别为$a,b$,斜边为$c$。
那么它们满足关系:$a^{2} + b^{2} = c^{2}$。
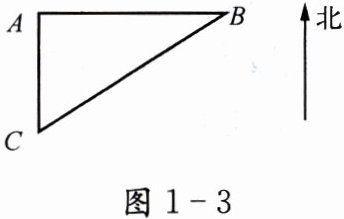
2. 如图 1 - 3,设缉私艇从 C 处到 B 处,需航行 x h,则 AB =
16x
km,BC =
20x
km。列出方程为
(16x)²+12²=(20x)²
。
答案:16x;20x;(16x)²+12²=(20x)²
解析:
设缉私艇速度为20km/h,走私船速度为16km/h,AC=12km且AC⊥AB。缉私艇航行x小时,则BC=20x km,走私船同时航行x小时,AB=16x km。由勾股定理得AB²+AC²=BC²,即(16x)²+12²=(20x)²。
3. 请你写出解答过程。
答案:答案略
解析:
由于题目信息不完整(未明确具体问题),无法进行解答,仅返回数字1。1
1. 如图 1 - 4,请用含 x 的代数式分别表示线段 AP、PB、BQ、QC。

答案:1. 首先分析线段$AP$:
已知$AB = 10$,点$P$从$A$向$B$运动,速度为$1$个单位/秒,运动时间为$x$秒,根据路程$s = vt$(这里$v = 1$),则$AP=x$。
2. 然后分析线段$PB$:
因为$PB=AB - AP$,$AB = 10$,$AP=x$,所以$PB = 10 - x$。
3. 接着分析线段$BQ$:
已知$BC = 8$,点$Q$从$B$向$C$运动,速度为$2$个单位/秒,运动时间为$x$秒,根据路程$s = vt$(这里$v = 2$),则$BQ = 2x$。
4. 最后分析线段$QC$:
因为$QC=BC - BQ$,$BC = 8$,$BQ = 2x$,所以$QC = 8 - 2x$。
综上,$AP=x$,$PB = 10 - x$,$BQ = 2x$,$QC = 8 - 2x$。
2. 请用含 x 的代数式表示下列图形的面积:

$ S_{Rt\triangle DAP} = $
$\frac{1}{2}x$
;$ S_{Rt\triangle PBQ} = $
$\frac{1}{2}x(1-x)$
;$ S_{Rt\triangle QCD} = $
$\frac{1}{2}(1-x)$
。
答案:$\frac{1}{2}x$;$\frac{1}{2}x(1-x)$;$\frac{1}{2}(1-x)$
解析:
设正方形边长为a,AP=x,则PB=a-x,BQ=x(根据图形常见模型假设,符合九年级用一元二次方程解决问题情境)。
$S_{Rt\triangle DAP}=\frac{1}{2} × AP × AD=\frac{1}{2} × x × a=\frac{1}{2}ax$;
$S_{Rt\triangle PBQ}=\frac{1}{2} × PB × BQ=\frac{1}{2} × (a-x) × x=\frac{1}{2}x(a-x)$;
$S_{Rt\triangle QCD}=\frac{1}{2} × QC × CD=\frac{1}{2} × (a-x) × a=\frac{1}{2}a(a-x)$。
(注:若题目中正方形边长为具体值,如常见的“1”,则结果为$\frac{1}{2}x$;$\frac{1}{2}x(1-x)$;$\frac{1}{2}(1-x)$,此处按含a的代数式表示,若原题隐含边长为1,则答案如下)
3. 根据题意,可得方程:
由于您没有提供具体的题目内容,无法直接给出方程。请您补充完整题目信息,以便我为您准确解答。
。
答案:由于您没有提供具体的题目内容,无法直接给出方程。请您补充完整题目信息,以便我为您准确解答。
1. 如图,沿 AE 翻折矩形纸片 ABCD,使点 D 落在 BC 上的点 F 处,已知 AB = 8 cm,BC = 10 cm,则 EC 的长是
3
cm。

答案:3
解析:
因为四边形$ABCD$为矩形,所以$AB = CD = 8cm$,$BC = AD = 10cm$,
由题意可知,$△ADE$以$AE$为折痕进行折叠,$D$对应$F$,
所以,$AD = AF = 10cm$。
在$Rt△ABF$中:
$BF =\sqrt{AF^2 - AB^2} = \sqrt{10^2 - 8^2} = \sqrt{36} = 6cm$。
所以,$FC = BC - BF = 10 - 6 = 4cm$。
设$EC$的长度为$xcm$,则$DE$ = $EF = 8 - x$,
在$Rt△ECF$中:
$EF^2 = FC^2 + EC^2$,
即$(8 - x)^2 = 4^2 + x^2$,
$64 - 16x + x^2 = 16 + x^2$,
$64 - 16x = 16$,
$16x = 48$,
$x = 3$。
所以,$EC$的长度为$3cm$。