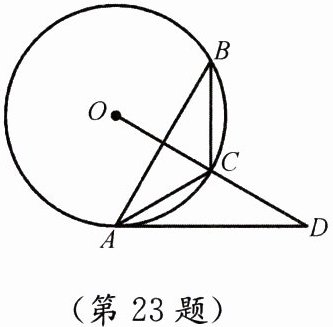
答案：(1) 是，理由如下：
连接$OA$，因为$\angle B = 30^{\circ}$，所以$\angle AOC = 2\angle B = 60^{\circ}$。
又因为$OA = OC$，所以$\triangle AOC$是等边三角形，$\angle OAC = \angle OCA = 60^{\circ}$。
已知$\angle CAD = 30^{\circ}$，所以$\angle OAD = \angle OAC + \angle CAD = 60^{\circ} + 30^{\circ} = 90^{\circ}$。
因此，$OA \perp AD$，又$OA$是$\odot O$的半径，所以$AD$是$\odot O$的切线。
(2) 因为$OD \perp AB$，所以$\angle AED = 90^{\circ}$，$\angle B = 30^{\circ}$，$BC = 5$，在$Rt\triangle BEC$中，$CE = \frac{1}{2}BC = \frac{5}{2}$。
因为$\triangle AOC$是等边三角形，所以$AC = OC = 5$，$AE = \frac{5\sqrt{3}}{2}÷2×2=\frac{5\sqrt{3}}{2}$（$30^{\circ}$所对直角边等于斜边一半，再根据勾股定理算出），$OA = 5$。
在$Rt\triangle OAD$中，$\angle OAD = 90^{\circ}$，$\angle D = \angle CAD = 30^{\circ}$，$OA = 5$，所以$AD = \sqrt{3}OA = 5\sqrt{3}$。
综上，$AD$的长为$5\sqrt{3}$。

答案：(1) 画树状图列举所有可能结果：开始球在甲手中，第一次传球有2种（乙、丙），第二次传球各有2种，第三次传球各有2种，共$2×2×2=8$种等可能结果。其中三次传球后球回到甲手中的结果有2种（甲→乙→丙→甲，甲→丙→乙→甲）。概率为$\frac{2}{8}=\frac{1}{4}$。
(2) 分情况计算三次传球后球到乙手中的概率：
开始在甲手中：树状图中到乙的结果有3种，概率$\frac{3}{8}$；
开始在乙手中：树状图中到乙的结果有2种，概率$\frac{2}{8}=\frac{1}{4}$；
开始在丙手中：与开始在甲手中对称，到乙的结果有3种，概率$\frac{3}{8}$。
因为$\frac{3}{8}＞\frac{1}{4}$，所以乙会让球开始时在甲或丙手中。
(1) $\frac{1}{4}$；(2) 甲或丙。