11. 已知$x = 1是关于x的一元二次方程x ^ { 2 } + a x + b = 0$的一个根,则代数式$a ^ { 2 } + b ^ { 2 } + 2 a b$的值是
1
.
答案:1
解析:
已知$x=1$是方程$x^{2}+ax+b=0$的一个根,代入得:
$1^{2}+a × 1+b=0$,
即$a+b=-1$。
需要求的代数式为$a^{2}+b^{2}+2ab$,根据完全平方公式可化简为:
$a^{2}+b^{2}+2ab=(a+b)^{2}$。
将$a+b=-1$代入得:
$(a+b)^{2}=(-1)^{2}=1$。
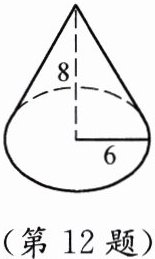
12. 如图,圆锥的底面半径为6cm,高为8cm,这个圆锥的侧面积是
60π
$c m ^ { 2 }$.
答案:$60\pi$
解析:
圆锥的底面半径$r = 6cm$,高$h = 8cm$,根据勾股定理,圆锥的母线长$l$(即斜高)为:
$l = \sqrt{r^{2} + h^{2}} = \sqrt{6^{2} + 8^{2}} = \sqrt{36 + 64} = \sqrt{100} = 10(cm)$。
圆锥的侧面积公式为$S = \pi r l$,将$r = 6cm$,$l = 10cm$代入公式得:
$S=\pi×6×10 = 60\pi(cm^{2})$。
13. 一组数据$x _ { 1 }$,$x _ { 2 }$,…,$x _ { n }$的方差为$s ^ { 2 }$,那么数据$x _ { 1 } - 5$,$x _ { 2 } - 5$,…,$x _ { n } - 5$的方差为
$s^2$
.
答案:$s^2$
解析:
设原数据的平均数为$\overline{x}$,则新数据的平均数为$\overline{x}-5$。原方差$s^2=\frac{1}{n}[(x_1-\overline{x})^2+\cdots+(x_n-\overline{x})^2]$,新方差为$\frac{1}{n}[(x_1-5-(\overline{x}-5))^2+\cdots+(x_n-5-(\overline{x}-5))^2]=\frac{1}{n}[(x_1-\overline{x})^2+\cdots+(x_n-\overline{x})^2]=s^2$
14. 在菱形$ABCD$中,$P是对角线AC$上的任意一点(不与$A$、$C$两点重合),以点$P为圆心的圆与AB$相切,则$AD与\odot P$的位置关系是
相切
.
答案:相切
解析:
∵四边形ABCD是菱形,∴AC平分∠DAB。∵以点P为圆心的圆与AB相切,∴点P到AB的距离等于⊙P的半径r。∵P在AC上,∴点P到AD的距离等于点P到AB的距离,即点P到AD的距离等于r。∴AD与⊙P相切。
15. 如图,在$Rt\triangle ABC$中,$\angle C = 9 0 ^ { \circ }$,$CA = CB = 2$,分别以点$A$、$B$、$C$为圆心,1为半径画弧,3条弧与$AB$所围成的阴影部分的周长是
π
.

答案:π
解析:
在$Rt\triangle ABC$中,$\angle C=90^\circ$,$CA=CB=2$,则$AB=2\sqrt{2}$,$\angle A=\angle B=45^\circ$。
以$A$为圆心、1为半径的弧:圆心角为$\angle A=45^\circ$,弧长$l_1=\frac{45\pi×1}{180}=\frac{\pi}{4}$。
以$B$为圆心、1为半径的弧:圆心角为$\angle B=45^\circ$,弧长$l_2=\frac{45\pi×1}{180}=\frac{\pi}{4}$。
以$C$为圆心、1为半径的弧:圆心角为$\angle C=90^\circ$,弧长$l_3=\frac{90\pi×1}{180}=\frac{\pi}{2}$。
阴影部分周长为$l_1+l_2+l_3=\frac{\pi}{4}+\frac{\pi}{4}+\frac{\pi}{2}=\pi$。
16. 如图,半圆$O的直径AB = 1 0 c m$,弦$AC = 6 c m$,$AD平分\angle BAC$,则$AD$的长为
4√5
.

答案:4√5
解析:
连接BC,∵AB是直径,∴∠ACB=90°。在Rt△ABC中,AB=10cm,AC=6cm,由勾股定理得BC=√(AB²-AC²)=√(10²-6²)=8cm。
以A为原点,AB为x轴建立坐标系,A(0,0),B(10,0),设C(x,y),则x²+y²=36,(x-10)²+y²=64,解得x=18/5,y=24/5,即C(18/5,24/5)。
设AD平分∠BAC,D到AC、AB距离相等,设D纵坐标为h(即到AB距离),则D(x1,h)。AC方程为y=(4/3)x,D到AC距离h=|4x1-3h|/5,得x1=2h,故D(2h,h)。
∵D在半圆上,圆心O(5,0),半径5,∴(2h-5)²+h²=25,解得h=4(h=0舍去),则D(8,4)。
AD=√(8²+4²)=√80=4√5 cm。
17. 解下列方程(每题4分,共12分)
(1)$7 ( 2 x - 3 ) ^ { 2 } = 2 8$;
(2)$2 x ^ { 2 } + 1 = 4 x$;
(3)$3 ( x - 2 ) ^ { 2 } = x ( x - 2 )$.
答案:(1)
已知$7(2x - 3)^{2}=28$,
则$(2x - 3)^{2}=4$,
$2x - 3=\pm2$,
当$2x - 3 = 2$时,$2x=5$,$x=\frac{5}{2}$;
当$2x - 3=-2$时,$2x = 1$,$x=\frac{1}{2}$。
所以方程的解为$x_{1}=\frac{5}{2}$,$x_{2}=\frac{1}{2}$。
(2)
已知$2x^{2}+1 = 4x$,
移项得$2x^{2}-4x + 1=0$,
其中$a = 2$,$b=-4$,$c = 1$,
根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$,
$\Delta=b^{2}-4ac=(-4)^{2}-4×2×1=16 - 8 = 8$,
$x=\frac{4\pm\sqrt{8}}{2×2}=\frac{4\pm2\sqrt{2}}{4}=\frac{2\pm\sqrt{2}}{2}$。
所以方程的解为$x_{1}=\frac{2+\sqrt{2}}{2}$,$x_{2}=\frac{2-\sqrt{2}}{2}$。
(3)
已知$3(x - 2)^{2}=x(x - 2)$,
移项得$3(x - 2)^{2}-x(x - 2)=0$,
提取公因式$(x - 2)$得$(x - 2)[3(x - 2)-x]=0$,
即$(x - 2)(3x-6 - x)=0$,
$(x - 2)(2x - 6)=0$,
则$x - 2=0$或$2x - 6=0$,
解得$x_{1}=2$,$x_{2}=3$。
18. (8分)已知关于$x的一元二次方程x ^ { 2 } - ( 2 k + 1 ) x + k ^ { 2 } + 2 k = 0有两个实数根x _ { 1 }$,$x _ { 2 }$. 求实数$k$的取值范围.
答案:
∵方程有两个实数根,
∴判别式$\Delta = [-(2k + 1)]^2 - 4×1×(k^2 + 2k) \geq 0$,
即$4k^2 + 4k + 1 - 4k^2 - 8k \geq 0$,
化简得$-4k + 1 \geq 0$,
解得$k \leq \frac{1}{4}$。
$k$的取值范围是$k \leq \frac{1}{4}$。