20. (12分)已知关于$x的一元二次方程x^{2}-(2k + 1)x + k^{2}+k = 0$.
(1) 求证:方程有两个不相等的实数根;
(2) 若$\triangle ABC的边AB$、$AC的长是方程x^{2}-(2k + 1)x + k^{2}+k = 0$的两个实数根,第三边$BC$的长为5,若$\triangle ABC$是等腰三角形,求$k$的值.
答案:(1)
证明:对于一元二次方程$x^{2}-(2k + 1)x + k^{2}+k = 0$,其中$a = 1$,$b=-(2k + 1)$,$c = k^{2}+k$。
$\Delta=b^{2}-4ac=[-(2k + 1)]^{2}-4×1×(k^{2}+k)$
$=4k^{2}+4k + 1-4k^{2}-4k$
$=1>0$
所以方程有两个不相等的实数根。
(2)
由求根公式$x=\frac{-b\pm\sqrt{\Delta}}{2a}$可得$x=\frac{2k + 1\pm1}{2}$,即$x_1=k + 1$,$x_2=k$。
因为$\triangle ABC$是等腰三角形,
当$AB=BC$时,$k + 1 = 5$,解得$k = 4$;
当$AC=BC$时,$k = 5$;
当$AB=AC$时,$k=k + 1$,无解。
综上,$k$的值为$4$或$5$。
21. (12分)如图,$AB是\odot O$的直径,$BC切\odot O于点B,CO交\odot O于点D,AD的延长线交BC于点E$.若$\angle C = 25^{\circ}$,求$\angle A$的度数.
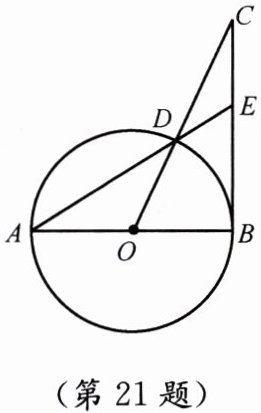
答案:∵BC切⊙O于点B,AB是⊙O的直径,
∴∠ABC=90°。
∵∠C=25°,
∴∠BOC=90°-∠C=65°。
∵OA=OD,
∴∠A=∠ADO。
∵∠BOC是△AOD的外角,
∴∠BOC=∠A+∠ADO=2∠A。
∴∠A=∠BOC/2=32.5°。
答:∠A的度数为32.5°。
解析:
∵BC切⊙O于点B,AB是⊙O的直径,
∴∠ABC=90°。
∵∠C=25°,
∴∠BOC=90°-∠C=65°。
∵OA=OD,
∴∠A=∠ADO。
∵∠BOC=∠A+∠ADO=2∠A,
∴∠A=32.5°。
22. (12分)如图,在$\triangle ABC$中,$AE$是角平分线,$\angle C = 90^{\circ},\angle B = 30^{\circ}$,点$D在边AB$上,$AD = 4$,以$AD为直径的\odot O经过点E$.
(1) 求证:$BC是\odot O$的切线;
(2) 求图中阴影部分的面积.

答案:(1) 证明见上;(2) 2√3 - 2π/3.
解析:
(1) 连接OE.
∵AD是⊙O的直径,AD=4,∴OA=OE=2,O为AD中点.
∵∠C=90°,∠B=30°,∴∠BAC=60°.
∵AE平分∠BAC,∴∠BAE=∠CAE=30°.
∵OA=OE,∴∠OEA=∠OAE=30°.
在△ABE中,∠BAE=30°,∠B=30°,∴∠AEB=180°-30°-30°=120°.
∴∠OEB=∠AEB-∠OEA=120°-30°=90°.
∴OE⊥BC.
∵OE是⊙O半径,∴BC是⊙O的切线.
(2) ∵∠OEB=90°,∠B=30°,OE=2,
∴OB=2OE=4,BE=√(OB²-OE²)=√(4²-2²)=2√3.
S△OEB=1/2×OE×BE=1/2×2×2√3=2√3.
∵∠AOE=180°-∠OAE-∠OEA=120°,
∴∠EOD=180°-∠AOE=60°.
S扇形OED=60°/360°×π×2²=1/6×4π=2π/3.
∴阴影部分面积=S△OEB-S扇形OED=2√3 - 2π/3.