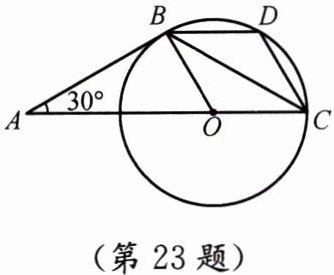
23. (12分)如图, $ AB $ 是 $ \odot O $ 的切线,切点为 $ B $,圆心 $ O $ 在 $ AC $ 上, $ \angle A = 30^{\circ} $, $ D $ 是 $ \overset{\frown}{BC} $ 的中点.
(1) 求证: $ AB = BC $.
(2) 四边形 $ BOCD $ 是菱形吗? 请说明理由.
答案:(1) 证明:
∵AB是⊙O的切线,切点为B,
∴OB⊥AB(切线垂直于过切点的半径),即∠ABO=90°。
在Rt△ABO中,∠A=30°,
∴∠AOB=90°-∠A=60°。
∵点O在AC上,
∴∠AOB+∠BOC=180°(平角定义),
∴∠BOC=180°-∠AOB=120°。
∵OB=OC(⊙O的半径),
∴∠OBC=∠OCB(等边对等角)。
在△OBC中,∠OBC+∠OCB+∠BOC=180°,
∴2∠OCB=180°-∠BOC=60°,即∠OCB=30°。
∵∠A=30°,
∴∠A=∠OCB,
∴AB=BC(等角对等边)。
(2) 四边形BOCD是菱形。理由如下:
连接OD。
∵D是弧BC的中点,
∴弧BD=弧DC,
∴∠BOD=∠DOC(等弧所对的圆心角相等)。
∵∠BOC=120°(已证),
∴∠BOD=∠DOC=60°。
∵OB=OD=OC(⊙O的半径),
∴△BOD和△DOC都是等边三角形(有一个角是60°的等腰三角形是等边三角形)。
∴BD=OB,DC=OC。
又∵OB=OC,
∴BD=OB=OC=DC。
∴四边形BOCD是菱形(四边相等的四边形是菱形)。
解析:
(1) 证明:
∵AB是⊙O的切线,
∴∠OBA=90°,
∵∠A=30°,
∴∠AOB=60°,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠AOB=∠OBC+∠OCB=2∠OCB,
∴∠OCB=30°,
∵∠A=∠OCB=30°,
∴AB=BC.
(2) 四边形BOCD是菱形.理由如下:
连接OD,
∵∠AOB=60°,
∴∠BOC=180°-∠AOB=120°,
∵D是$\overset{\frown}{BC}$的中点,
∴$\overset{\frown}{BD}=\overset{\frown}{CD}$,
∴∠BOD=∠COD=60°,
∵OB=OD=OC,
∴△BOD和△COD都是等边三角形,
∴OB=BD=DC=OC,
∴四边形BOCD是菱形.
24. (12分)如图, $ AB $ 为 $ \odot O $ 的直径, $ AB \perp AC,BC $ 交 $ \odot O $ 于点 $ D,E $ 是 $ AC $ 的中点, $ ED $ 与 $ AB $ 的延长线相交于点 $ F $.
(1) 求证: $ DE $ 是 $ \odot O $ 的切线;
(2) 已知 $ \angle F = 30^{\circ},BF = 1 $,求 $ \triangle ABC $ 外接圆的半径.

答案:
(1) 连接 $OD$,$AD$。
∵ $AB$ 为 $\odot O$ 直径,
∴ $\angle ADB = 90^\circ$,则 $\angle ADC = 90^\circ$。
∵ $E$ 是 $AC$ 中点,
∴ $DE = AE = \frac{1}{2}AC$,
∴ $\angle EAD = \angle EDA$。
∵ $OA = OD$,
∴ $\angle OAD = \angle ODA$。
∵ $AB \perp AC$,
∴ $\angle OAC = 90^\circ$,即 $\angle OAD + \angle EAD = 90^\circ$。
∴ $\angle ODA + \angle EDA = 90^\circ$,即 $\angle ODE = 90^\circ$。
∵ $OD$ 是 $\odot O$ 半径,
∴ $DE$ 是 $\odot O$ 的切线。
(2) 设 $\odot O$ 半径为 $r$,则 $OD = OB = r$,$AB = 2r$,$OF = OB + BF = r + 1$。
∵ $DE$ 是切线,
∴ $OD \perp DE$。在 $Rt\triangle ODF$ 中,$\angle F = 30^\circ$,
∴ $\angle DOF = 60^\circ$,$OD = \frac{1}{2}OF$,即 $r = \frac{1}{2}(r + 1)$,解得 $r = 1$。
∵ $OD = OB$,$\angle DOF = 60^\circ$,
∴ $\triangle OBD$ 是等边三角形,$\angle OBD = 60^\circ$。
在 $Rt\triangle ABD$ 中,$\angle BAD = 30^\circ$,$AB = 2r = 2$,
∴ $AD = AB \cdot \cos 30^\circ = \sqrt{3}$。
∵ $\angle CAD = 90^\circ - 30^\circ = 60^\circ$,$E$ 为 $AC$ 中点,$\angle ADC = 90^\circ$,
∴ $AE = AD = \sqrt{3}$,$AC = 2AE = 2\sqrt{3}$。
在 $Rt\triangle ABC$ 中,$BC = \sqrt{AB^2 + AC^2} = \sqrt{2^2 + (2\sqrt{3})^2} = 4$。
∵ $\triangle ABC$ 是直角三角形,外接圆半径为斜边一半,
∴ 半径为 $\frac{BC}{2} = 2$。
25. (12分)如图,在菱形 $ ABCD $ 中, $ AB = 2\sqrt{3},\angle A = 60^{\circ},\odot D $ 与 $ AB $ 相切于点 $ E $.
(1) 求证: $ \odot D $ 与边 $ BC $ 也相切;
(2) 设 $ \odot D $ 与 $ BD $ 相交于点 $ H $,与边 $ CD $ 相交于点 $ F $,连接 $ HF $,求图中阴影部分的面积(结果保留 $ \pi $);
(3) $ \odot D $ 上的一动点 $ M $ 从点 $ F $ 出发,按逆时针方向运动半周,当 $ S_{\triangle HDF}= \sqrt{3}S_{\triangle MDF} $ 时,求动点 $ M $ 经过的弧长(结果保留 $ \pi $).

答案:(1) 见解析;(2) 3π/2 - 9√3/4;(3) π/2或5π/2。
解析:
(1) 证明:连接DE,∵AB与⊙D相切于E,∴DE⊥AB,DE为半径。在菱形ABCD中,AD=AB=2√3,∠A=60°,∴DE=AD·sin60°=2√3×(√3/2)=3。过D作DG⊥BC于G,∵∠C=∠A=60°,CD=2√3,∴DG=CD·sin60°=2√3×(√3/2)=3,即D到BC距离=半径,∴⊙D与BC相切。
(2) ∵DF=3(半径),BD为菱形对角线,∠A=60°,△ABD为等边三角形,BD=2√3,DH=3。∠HDF=60°(∠CDB=60°)。扇形DHF面积=60/360×π×3²=3π/2。△DHF面积=√3/4×3²=9√3/4。阴影面积=3π/2 - 9√3/4。
(3) S△MDF=9/4,设M到DF距离h=3/2。⊙D中y=3/2,x=±3√3/2。F(3,0),M1(3√3/2,3/2)对应圆心角30°,弧长=30π×3/180=π/2;M2(-3√3/2,3/2)对应圆心角150°,弧长=150π×3/180=5π/2。