1. 爷爷饭后出去散步,从家里出发 20 min 后到一个离家 900 m 的街心花园,与朋友在原地聊天 10 min 后,用 15 min 返回家里.下列四个图象中,能表示爷爷离家的距离 y m 与离家时间 x min 之间函数关系的是 ()

2. 甲、乙两人以相同路线前往距离单位 10 km 的培训中心参加学习.图中 lₐ,lᵦ分别表示甲、乙两人前往目的地所走的路程 s km 随时间 t min 变化的函数图象.乙出发______min 后追上甲.

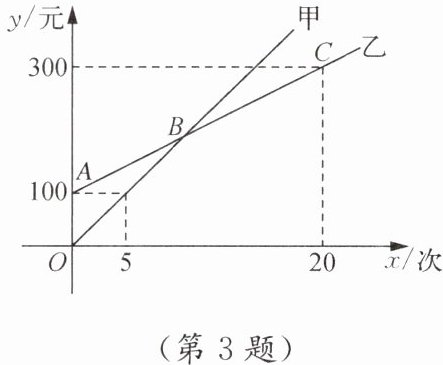
3. 某生态体验园推出了甲,乙两种消费卡,设入园次数为 x 次,所需费用为 y 元,选择这两种卡消费时,y 与 x 的函数关系如图所示,解答下列问题：
(1)分别求出选择这两种卡消费时,所需费用 yₐ元、yᵦ元关于入园次数 x 次的函数表达式；
(2)当消费多少次时,甲、乙两种消费卡的费用相同？
(3)若进入生态体验园 15 次,采用哪种方式比较划算？

(1)设$y_{甲}=k_{1}x$，把(5，100)代入，得$5k_{1}=100$，解得$k_{1}=20$，所以$y_{甲}=20x$。
设$y_{乙}=k_{2}x+b$，把(0，100)，(20，300)代入，得$\begin{cases}b=100,\\20k_{2}+b=300.\end{cases}$解得$\begin{cases}k_{2}=10,\\b=100.\end{cases}$所以$y_{乙}=10x + 100$。
(2)令$y_{甲}=y_{乙}$，即$20x=10x + 100$，$20x-10x=100$，$10x=100$，解得$x = 10$。
所以当消费10次时，甲、乙两种消费卡的费用相同。
(3)当$x = 15$时，$y_{甲}=20×15=300$，$y_{乙}=10×15 + 100=250$。
因为$300＞250$，所以采用乙种方式比较划算。

1. 如图是光线从空气进入水中的光路图,若按如图所示的方式建立平面直角坐标系,并设入水前与入水后光线所在直线的函数表达式分别为$ y_1= k_1x,y_2= k_2x,$则下列关于$ k_1$与$ k_2$关系的说法中,正确的是 ( )
$A. k_2＜0＜k_1$
$B. k_1＜0＜k_2$
$C. k_1＜k_2＜0$
$D. k_2＜k_1＜0$