11. 如图,在 $\triangle ABC$ 中,$\angle ACB= 90^\circ$,$AB= 5\ cm$,$BC= 4\ cm$,若点 $P$ 从点 $A$ 出发,以每秒 $2\ cm$ 的速度沿折线 $A-B-C-A$ 运动,设运动时间为 $t$ 秒($t>0$).
(1)若点 $P$ 在 $BC$ 上,且满足 $PA= PB$,求此时 $t$ 的值;
(2)若点 $P$ 恰好在 $\angle ABC$ 的平分线上,求此时 $t$ 的值;
(3)在点 $P$ 运动过程中,当 $t$ 为何值时,$\triangle ACP$ 为等腰三角形.
答案:(1)如图
(1),设PB = PA = x cm,则PC = (4 - x)cm,
∵∠ACB = 90°,AB = 5 cm,BC = 4 cm,
∴AC = 3 cm。在Rt△ACP中,$AC^{2}+PC^{2}=AP^{2}$,
∴$3^{2}+(4 - x)^{2}=x^{2}$,解得$x=\frac{25}{8}$,
∴$BP=\frac{25}{8}$cm,
∴$t=\frac{AB + BP}{2}=\frac{5+\frac{25}{8}}{2}=\frac{65}{16}$。
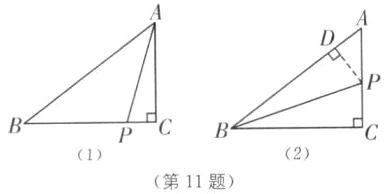
(2)如图
(2),过点P作PD⊥AB于点D。
∵BP平分∠ABC,∠C = 90°,
∴PD = PC。
∵BP = BP,
∴Rt△BPD≌Rt△BPC(HL),
∴BC = BD = 4 cm,
∴AD = 5 - 4 = 1(cm)。设PD = PC = y cm,则AP = (3 - y)cm,在Rt△ADP中,$AD^{2}+PD^{2}=AP^{2}$,
∴$1^{2}+y^{2}=(3 - y)^{2}$,解得$y=\frac{4}{3}$,
∴$CP=\frac{4}{3}$cm,
∴$t=\frac{AB + BC + CP}{2}=\frac{5 + 4+\frac{4}{3}}{2}=\frac{31}{6}$;当点P与点B重合时,点P也在∠ABC的平分线上,此时,$t=\frac{AB}{2}=\frac{5}{2}$。综上所述,点P恰好在∠ABC的平分线上时,t的值为$\frac{31}{6}$或$\frac{5}{2}$。
(3)分四种情况:
①如图
(3),当P在AB上,且AP = CP时,

∠A = ∠ACP,而∠A + ∠B = 90°,∠ACP + ∠BCP = 90°,
∴∠B = ∠BCP,
∴CP = BP,
∴P是AB的中点,即$AP=\frac{1}{2}AB=\frac{5}{2}$cm,
∴$t=\frac{AP}{2}=\frac{5}{4}$;
②如图
(4),当P在AB上且AP = CA = 3 cm时,$t=\frac{AP}{2}=\frac{3}{2}$;
③如图
(5),当P在AB上且AC = PC时,过点C作CD⊥AB于点D,则$CD=\frac{AC\cdot BC}{AB}=\frac{12}{5}$cm,

∴在Rt△ACD中,$AD=\frac{9}{5}$cm,
∴$AP = 2AD=\frac{18}{5}$cm,
∴$t=\frac{AP}{2}=\frac{9}{5}$;
④如图
(6),当P在BC上且AC = PC = 3 cm时,BP = 4 - 3 = 1(cm),
∴$t=\frac{AB + BP}{2}=\frac{6}{2}=3$。
综上所述,当$t=\frac{5}{4}$或$\frac{3}{2}$或$\frac{9}{5}$或3时,△ACP为等腰三角形。