12. 中考新考法 操作探究 [问题情境]小明用4张全等的直角三角形纸片拼成图(1),利用此图,可以验证勾股定理吗？
[初步运用](1)如图(1),若b= 2a,则小正方形面积：大正方形面积= .
(2)现将图(1)中上方的两直角三角形向内折叠,如图(2),若a= 4,b= 6,则此时空白部分的面积为.
[迁移运用]用三张含60°角的全等三角形纸片,能否拼成一个特殊图形呢？带着这个疑问,小丽拼出图(3)的等边三角形,你能否仿照勾股定理的验证,发现含60°角的三角形三边a,b,c之间的关系,写出此等量关系式及其推导过程.(知识补充：如图(4),含60°角的直角三角形的对边长y：斜边长x= 定值k)

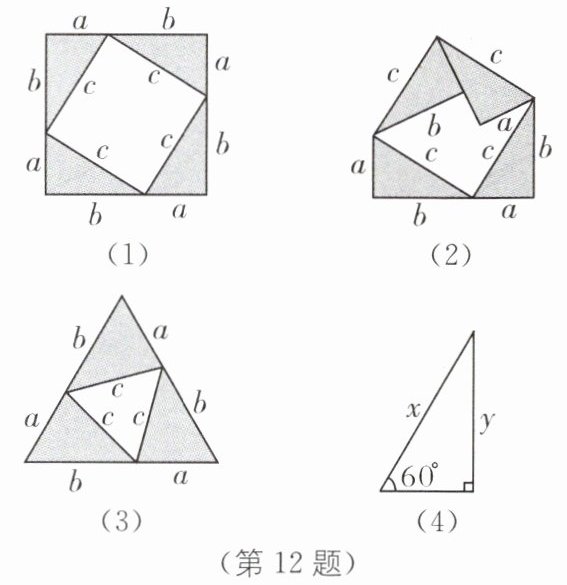
结论:a²+b²−ab=c².理由如下:
由题意，得大正三角形的面积=3个全等三角形的面积+小正三角形的面积,
∴$\frac{1}{2}$(a+b)·k(a+b)=3×$\frac{1}{2}$b·ka+$\frac{1}{2}$c·ck,
∴(a+b)²=3ab+c²,
∴a²+b²−ab=c².

13. 中考新考法 类比探究 (2025·南通海门区期末)在△ABC中,BC= a,AC= b,AB= c,且c≥b≥a.
(1)当△ABC是锐角三角形时,小明猜想：$a^{2}+b^{2}＞c^{2}$. 以下是他的证明过程：
如图(1),过点A作AD⊥CB,垂足为D.
设CD= x.
∵在Rt△ADC中,$AD^{2}= b^{2}-x^{2}$,
在Rt△ADB中,$AD^{2}= $①______,
∴$b^{2}-x^{2}= $①______.
化简,得$a^{2}+b^{2}-c^{2}= 2ax$.
∵a＞0,x＞0,∴②______＞0,
∴$a^{2}+b^{2}-c^{2}＞0$,
∴$a^{2}+b^{2}＞c^{2}$.
其中,①是______,②是______.
(2)如图(2),当△ABC是钝角三角形时,猜想$a^{2}+b^{2}与c^{2}$之间的关系并证明.