2025年实验班提优训练八年级数学上册苏科版第21页解析答案

8.如图,已知 AB= AC,AD= AE,BE= CD.
(1)求证:∠BAC= ∠EAD;
(2)写出∠1,∠2,∠3 之间的数量关系,并予以证明.
]

答案：
(1)在△BAE和△CAD中,$\left\{\begin{array}{l} AE=AD,\\ AB=AC,\\ BE=CD,\end{array}\right.$
∴△BAE≌△CAD(SSS).
∴∠BAE=∠1.
∴∠BAE+∠EAC=∠1+∠EAC.
∴∠BAC=∠EAD.
(2)∠3=∠1+∠2.证明如下:
∵△BAE≌△CAD,
∴∠1=∠BAE、∠2=∠ABE.
∵∠3=∠BAE+∠ABE,
∴∠3=∠1+∠2.

9.中考新考法添加条件开放 (2024·浙江杭州西湖区期末)如图,在△ABC 和△DEF 中,点 B,E,C,F 在同一条直线上,已知∠B= ∠DEF,BE= CF.下面给出四个条件:①AC= DF;②AB= DE;③AC//DF;④∠A= ∠D.请你从中任选一个条件,使得△ABC≌△DEF,并写出证明过程.
]

答案：选②AB=DE(答案不唯一).证明如下:
∵BE=CF,
∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中,$\left\{\begin{array}{l} BC=EF,\\ ∠B=∠DEF,\\ AB=DE,\end{array}\right.$
∴△ABC≌△DEF(SAS).

10.(2025·南京鼓楼区求真中学期中)已知:如图(1),在△ABC 中,∠ABC= 45°,H 是高 AD,BE 所在直线的交点.

(1)求证:BH= AC;
(2)如图(2),若∠A 改成钝角后,结论 BH= AC 还成立吗? 若成立,请补全图形并证明,若不成立,请说明理由.

答案：

(1)由题意可知,∠ADC=∠BEC=∠BDH=90°,
∴∠DAC+∠C=90°,∠EBC+∠C=90°,
∴∠DAC=∠EBC.
∵∠ABC=45°,
∴∠BAD=90°−∠ABC=90°−45°=45°,
∴∠ABC=∠BAD,
∴△ABD是等腰直角三角形,
∴AD=BD.在△BDH和△ADC中,$\left\{\begin{array}{l} ∠DBH=∠DAC,\\ BD=AD,\\ ∠BDH=∠ADC,\end{array}\right.$
∴△BDH≌△ADC(ASA),
∴BH=AC.
(2)HB=AC仍然成立.理由如下:补全图形如图，

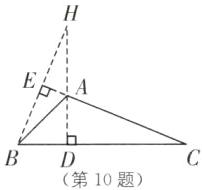
由题意可知,∠HDB=∠CDA=∠CEB=90°,
∴∠H+∠HAE=90°,∠C+∠CAD=90°.又∠HAE=∠DAC,
∴∠H=∠C.
∵∠ABC=45°,∠ADB=90°,
∴三角形ABD是等腰直角三角形,
∴AD=BD.在△BDH和△ADC中,$\left\{\begin{array}{l} ∠H=∠C,\\ ∠HDB=∠CDA,\\ BD=AD,\end{array}\right.$
∴△BDH≌△ADC(AAS),
∴BH=AC.