1. 比较两条线段的长短常用的方法有
度量
法和
叠合
法.
答案:度量 叠合
2. 如果一个点把一条线段分成两条
相等
的线段,那么这个点叫作这条线段的中点.
答案:相等
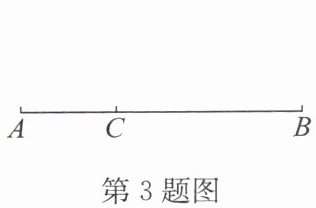
3. 因为图中 C 是线段 AB 的中点,所以 $ AC = BC = $
$\frac{1}{2}$
$ AB $ 或 $ AB = $
2
$ AC = $
2
$ BC $.
答案:$\frac{1}{2}$ 2 2
解析:
解:因为图中 C 是线段 AB 的中点,所以 $ AC = BC = \frac{1}{2}AB $ 或 $ AB = 2AC = 2BC $。
$\frac{1}{2}$ 2 2
1. 如图①,已知线段 $ a,b $,图②中线段 AB 表示的是 (
D
)
A.$ a - b $
B.$ a + b $
C.$ a - 2b $
D.$ 2a - b $
答案:D
解析:
由图②可知,从点A到第一个分点的长度为$a$,从第一个分点到点C的长度为$a$,所以A到C的总长度为$a + a = 2a$。又因为点B到点C的长度为$b$,所以线段AB的长度为A到C的长度减去B到C的长度,即$2a - b$。
D
2. 如图,填空:
(1)$ AC = BC + (
AB
); (2)$ CD = AD - (
AC
);
(3)$ CD = (
BD
) $ - BC $; (4)$ AB + BC = (
AD
) $ - CD $.
答案:(1)AB (2)AC (3)BD (4)AD
3. 如图,$ AC = \frac{1}{2}BC $.

(1)若 $ AB = 12 \text{ cm} $,则 $ BC = $
8
$\text{cm} $,$ AC = $
4
$\text{cm} $;
(2)若 $ AB = 15 \text{ cm} $,则 $ AC = $
5
$\text{cm} $,$ BC = $
10
$\text{cm} $.
答案:(1)8 4 (2)5 10
4. 如图,$ DB = 3 \text{ cm} $,$ BC = 7 \text{ cm} $,C 是 AD 的中点,求 AB 的长.

答案:解:因为BC=7cm,DB=3cm,
所以CD=BC−DB=7−3=4(cm).
因为C是AD的中点,
所以AD=2CD=2×4=8(cm),
所以AB=AD+DB=8+3=11(cm),
即AB的长为11cm.
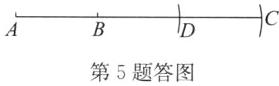
5. 如图,已知线段 AB.
(1)请用尺规按要求作图:延长线段 AB 至点 C,使得 $ BC = 2AB $;(不写作法,保留作图痕迹)
(2)若 $ AB = 3 \text{ cm} $,求线段 AC 的长.

答案:(1)如答图,BC就是所求作的线段.
(2)由(1)知,BC=2AB.因为AB=3cm,
所以BC=2AB=2×3=6(cm),
所以AC=AB+BC=3+6=9(cm),
即线段AC的长为9cm.