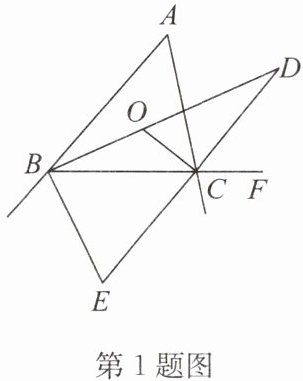
1. 如图,在$△ABC$中,$∠ABC与∠ACB$的平分线交于点O,$∠ACB的外角平分线所在的直线与∠ABC$的平分线相交于点D,与$∠ABC$的外角平分线相交于点E,有下列结论:①$∠BOC= 90^{\circ }+\frac {1}{2}∠A$;②$∠D= \frac {1}{2}∠A$;③$∠A= \frac {2}{3}∠E$;④$∠E+∠DCF= 90^{\circ }+∠ABD$.其中一定正确的是( )
A.①②④
B.①②③
C.①②
D.①②③④
答案:1.A 点拨:∵∠ABC,∠ACB的平分线交于点O,
∴∠ABD=∠OBC=$\frac{1}{2}$∠ABC,∠OCB=∠OCA=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°−∠A)=90°−$\frac{1}{2}$∠A,
∴∠BOC=180°−(∠OBC+∠OCB)=180°−(90°−$\frac{1}{2}$∠A)=90°+$\frac{1}{2}$∠A,故①正确;
∵CD平分∠ACF,∴∠DCF=$\frac{1}{2}$∠ACF,
∴∠ACF=∠ABC+∠A,∠DCF=∠OBC+∠D,
∴2∠OBC+2∠D=∠ABC+∠A,
∴∠D=$\frac{1}{2}$∠A,故②正确;
如答图,∵∠MBC=∠A+∠ACB,∠BCN=∠A+∠ABC,∠ACB+∠A+∠ABC=180°,
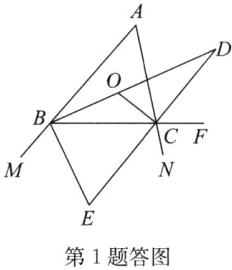
∴∠MBC+∠NCB=∠A+∠ACB+∠A+∠ABC=180°+∠A.
∵BE平分∠MBC,CE平分∠BCN,
∴∠MBC=2∠EBC,∠BCN=2∠BCE,
∴∠EBC+∠BCE=90°+$\frac{1}{2}$∠A,
∴∠E=180°−∠EBC−∠ECB=180°−90°−$\frac{1}{2}$∠A=90°−$\frac{1}{2}$∠A,
∴∠A=180°−2∠E,故③错误;
∵∠DCF=∠DBC+∠D,∴∠E+∠DCF=90°−$\frac{1}{2}$∠A+∠DBC+$\frac{1}{2}$∠A=90°+∠DBC.
∵∠ABD=∠DBC,
∴∠E+∠DCF=90°+∠ABD,故④正确.