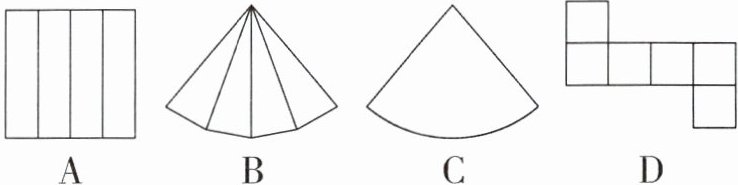
1.(2024·常州中考)下列图形中,为四棱锥的侧面展开图的是 (
B
)
答案:B
解析:
四棱锥的侧面由4个三角形组成,且这4个三角形有一个公共顶点。观察各选项:
A是长方形,为棱柱侧面展开图;
B是4个有公共顶点的三角形,符合四棱锥侧面展开图特征;
C是1个扇形,为圆锥侧面展开图;
D是正方形组合,为正方体表面展开图。
答案:B
2.(2023·达州中考)下列图形中,可以折叠成长方体的是 (
C
)
答案:C
3.(2024·德阳中考)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日.在一次综合实践活动中,一同学用如图所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样.则在A,B,C处依次写上的字可以是 (
A
)
A.吉 如 意
B.意 吉 如
C.吉 意 如
D.意 如 吉
答案:A
解析:
解:根据题意,正方形为底面,侧面有一个三角形写“祥”字,旋转时看到“吉祥如意”。分析图形折叠后各三角形的位置顺序,A、B、C处依次应为“吉”“如”“意”。
答案:A
4.下列表面展开图对应的立体图形的名称分别是:
圆柱
圆锥
三棱锥
长方体
答案:圆柱 圆锥 三棱锥 长方体
5.(1)底面圆半径为1、高为2的圆柱体,其侧面展开图的周长是
4π+4
.(结果保留π)
(2)圆柱的侧面展开图是边长为4的正方形,则圆柱的体积是
$\frac{16}{π}$
.(结果保留π)
答案:(1)4π+4 (2)$\frac{16}{π}$
解析:
(1)圆柱底面圆半径为1,底面圆周长为$2\pi r = 2\pi×1 = 2\pi$,侧面展开图为长方形,长为底面圆周长$2\pi$,宽为圆柱的高2,所以侧面展开图的周长为$2×(2\pi + 2)=4\pi + 4$。
(2)圆柱侧面展开图是边长为4的正方形,所以圆柱的高$h = 4$,底面圆周长$2\pi r = 4$,解得$r=\frac{2}{\pi}$,圆柱体积$V=\pi r^2h=\pi×(\frac{2}{\pi})^2×4=\pi×\frac{4}{\pi^2}×4=\frac{16}{\pi}$。
(1) $4\pi + 4$
(2) $\frac{16}{\pi}$
6.现有一正方体形状的无盖纸盒,在盒底上印有一个兑奖的标志“囍”字,如图①所示.现请同学们用剪刀沿这个正方体纸盒的棱将这个纸盒剪开,使之展开成一平面图形,那么能剪出许多种不同情况的展开图.图②是其中一种展开图,请再画出两种不同情况,要求展开图中的标志“囍”字是正立着的.

答案:答案合理即可,示例:如图所示。

7.如图所示的是一个正方体的表面展开图,折成正方体后其相对面上的两个数互为相反数,求a - b的值.

答案:由题意得a+c的相对面上是−2,c的相对面上是3,b的相对面上是−1,所以c=−3,b=1,a+c=2,即a=5,所以a−b=4。
解析:
解:由正方体表面展开图可知,相对面为:$a+c$与$-2$,$c$与$3$,$-1$与$b$。
因为相对面上的两个数互为相反数,
所以$c=-3$,$b=1$,$a+c=2$。
由$a+c=2$,$c=-3$,得$a=2 - c=2 - (-3)=5$。
则$a - b=5 - 1=4$。
答案:$4$
8.(2024·江西中考)如图是4×3的正方形网格,选择一空白小正方形,能与阴影部分组成正方体展开图的方法有 ( )

A.1种
B.2种
C.3种
D.4种
答案:B 解析:如图所示,共有2种方法,故选B。
